Mutagenesis and sex ratio in Drosophila melanogaster.

Ivanov, Yu. N.  Institute of Cytology and Genetics, Siberian Division of Russian Academy of Sciences, Novosibirsk, 630090, Russia. FAX: (3832)33 12 78. E-mail: iyn@bionet.nsc.ru.

According to Catcheside and Lea (1945), already the first researchers of mutagenesis (Muller, 1928, 1940;  Hanson, 1928;  Gowen and Gay, 1933;  Bauer, 1939;  Catcheside and Lea, 1945) found that when males of D. melanogaster were irradiated, in their  progeny a reduction of sex ratio  was observed, i.e. the numerical female to male ratio decreased as compared to non-irradiated control. (Here and below,  stands for the 1^st generation, and  for its parents.) Catcheside and Lea summarized the data of all authors and found that the dependence of the sex ratio on the dose of irradiation of  males in Roentgens was a decreasing function , where  is the sex ratio in the control. If one assumes that the function  is fit for all possible doses, then it seems that increasing the dose one can decrease the sex ratio practically to zero.

A usual consequence of mutagenesis is formation of dominant lethal mutations (DLM), which reduce the number of  offspring of mutagen-treated parents; therefore, it is natural to attribute the reduction of the sex ratio in mutagenesis to the effect of DLM that is selective with respect to sex (Catcheside and Lea, 1945;  Hadorn, 1961;  Ivanov, 1998a, b). According to the common notion, DLM are deletions of euchromatin (McClintock, 1941;  Hadorn, 1961) and its point damages (usually genic mutations) (Ivanov, 1998b) with immediate lethal effect in the very first zygote. If the lethal effect of the mutation is not manifested in the first zygote, which it entered after its formation, such mutation is not recorded as a DLM, even if it turns out to be lethal in subsequent generations. The mutation is called dominant lethal only because it displays a lethal effect in heterozygote, although it would have turned out to be an ordinary recessive lethal or visible mutation had it not been eliminated immediately as DLM.

The theory explains the described shift of the sex ratio as follows. Due to the fact that the changes induced in the euchromatin X chromosome of X spermia make a greater contribution to DLM than the changes induced in the heterochromatin Y chromosome of Y spermia do, a mutagen-treated male transmits the obtained injuries more often to his daughters XX than to his sons XY. (Bold letters here designate chromosomes brought into the zygote by the male, i.e. mutagen-treated ones.) That is why in  females die more frequently than males and sex ratio decreases. The higher the mutagen dose, the more DLM arise, and the more the sex ratio must decrease, so that it could serve as a measure for the number of DLM.

Using these assumptions, the author has worked out a schedule of experiments for estimating the average number of DLM in the genome of D. melanogaster (Ivanov, 1998a, b) in order to confirm and specify the estimate of the number of DLM obtained earlier by a more direct method – by zygote survival (Ivanov, 1998c). Already the first three experiments gave not quite satisfactory results, since the treatment of  males with ethylmethane sulphonate (EMS) (equivalent by its mutability in the X chromosome to a 19350 R g-irradiation) and with g-irradiation in the doses of 1500 and 2500 R gave

smaller deviations from the normal sex ratio than it was expected, so that the estimates of the  average  DLM number per genome turned out to be understated.  Wanting  to  obtain

more reliable results, the author replicated the experiment twice at higher g-ray doses, using in one case (strain Oregon-R) irradiation of females as control.

The results were unexpected and discouraging. They were so puzzling that doubts arose concerning the correctness of dosage, which, however, turned out to be absolutely unwarranted. Firstly, despite the dose of 7000 R, the sex ratio did not change. Secondly, it was expected that irradiation of females would cause an increase of the sex ratio, since all the recessive lethals induced in female’s X chromosomes, having got into hemizygote in her sons, had to behave as DLM and reduced the number of males. However, there were no symptoms thereof.

Studies of the effect of g-irradiation of  males and females on the sex ratio were specially continued on a rather large number of cultures and flies in the cultures and at considerable irradiation doses (up to 15000 R), but without any effect predicted by the theory. All the author’s data on sex ratio in  under the influence of mutagens on males are presented in Table 1, and on females, in Table 2.

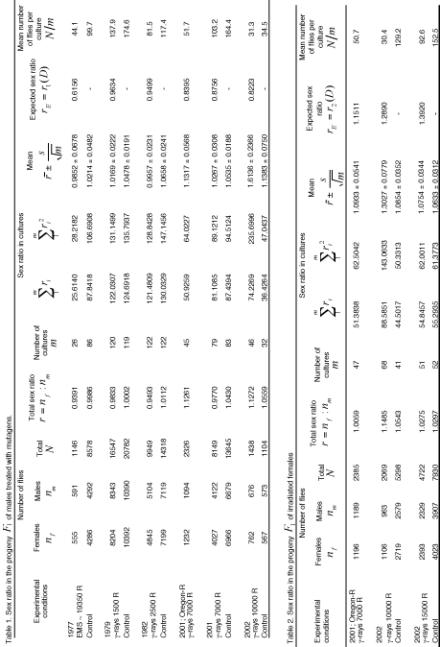
In the two tables, the column “Experimental conditions” indicates the year, fly strain and irradiation dose: no indication means the strain Canton-S, but the use of Oregon-R is indicated. The control always represents replication of the experiment presented in the line situated above, but without irradiation. Columns with sums  and  are presented for the sake of convenience of variance analysis.

The expected sex ratio in Table 1 and 2 was calculated differently. In irradiation of males (Table 1) it was calculated by Catcheside and Lea formula

                                                                                       (1)

where  is the total sex ratio in the control. In the absence of ordinary control, it was assumed that . In irradiation of females (Table 2), for  it was necessary to use a different formula deduced as follows.

Dependence of the average number  of recessive lethal mutations (RLM) and visible mutations (VM) induced in X chromosome of males on the irradiation dose  in R is described by a linear function

            ,                                                                    (2)

which was obtained from all our experiments on measurement of mutability in male’s X chromosome at various doses of g-irradiation. (Its coefficients with errors are  and .) Let us assume that dependence of mutability on the dose in ova is the same as that in spermia. Since RLM arising in ova affect males like DLM do, because they turn out to be in hemizygote, in order to take into account the death of males due to irradiation of parental females, let us find the dependence of the average number  of RLM induced in the X chromosome of ova on the irradiation dose . RLM make up  of the whole number of arising RLM and VM, therefore the sought relation will be expressed by the formula

            .                                                   (3)

Let us designate in the equation (3) the free term, or the number of spontaneous RLM in X chromosome, as , and the coefficient as . The probability of survival of a male produced by non-irradiated parents is , where  is the frequency of arising of spontaneous RLM in X chromosome. The probability of survival of a male produced by female irradiated with a dose  is , where  is the frequency of arising of RLM in X chromosome induced by the dose . Let the sex ratio without irradiation be equal to unit,  and  be the proportions of females and males in the progeny of females irradiated with the dose , respectively, and  be the multiplicity of decrease of the proportion of flies of each sex due to mutations (autosomal etc.) equally affecting the mortality of both sexes, at the dose . Then the expected sex ratio in irradiation of female with the dose  is

.

The multiplier  in the numerator is necessary to make the sex ratio without irradiation equal to 1. Substituting the numerical value  into the obtained expression and introducing the multiplier , which corrects the result for the total sex ratio in the control, we obtain definitely:

                        .                                                               (4)

It is by this formula that theoretically expected sex ratio in Table 2 was calculated.

Now one can see that the real sex ratio in mutagenesis is different from the expected one, most often conserving value close to unit, i.e. it does not obey the tendency predicted by the theory. If the reader finds that the assumptions under which formula (4) for the case of irradiated females was obtained are not quite correct, let him compare the real sex ratio with irradiation of females not with the theoretically expected one, but with the control. The equal sex ratios in the experiment and in the control also demonstrate inconsistency of the theory according to which it must change due to mutagenesis.

The use of high doses of mutagens usually causes a considerable mortality of flies due to induction of DLM, the population density in cultures decreasing extremely, which probably could tell on the sex ratio. For this reason, for compensation of flies’ death from DLM and for at least a relative leveling of population density in cultures in the experiment and in the control, at high irradiation doses we put into cultures many parental females – often over 20 – instead of the usual 1 – 2 in control cultures. The columns of tables entitled “Mean number of flies in culture ” show how useful this turned out to be. Thanks to this, the total number of flies in experiments increased considerably. The first researchers did not resort to such measures, and, probably, it is because of this that they obtained results different from ours. So, Catcheside and Lea (1945) obtained their sex ratio of  for the highest dose of 11420 R on only 13 flies.

Let us first consider the experiments with mutagenic treatment of males (Table 1).

Chi-square test shows a statistically significant heterogeneity of the total sex ratio  in the total set of all the experimental and control samples ( at , ). The same test shows a statistically significant heterogeneity of the set of experimental samples ( at , ) and homogeneity of control samples ( at ), wherefrom it follows that the heterogeneity of the total sex ratio is caused by the mutagens, but not by any other factor.

Variance analysis leads to the same conclusions for the average sex ratio in cultures. The hypothesis of equality of mean values for sex ratio in all the experimental samples is discarded as incredible at the significant level of , but the same hypothesis for control samples is not rejected. In two-way analysis, no influence of the general experimental conditions on the sex ratio is found, and the influence of mutagenic treatment of males is rather significant ( ). For the sake of brevity, variance analysis is not presented, but it is easy to reconstruct it since Table 1 and 2 contain all necessary data.

Although the influence of mutagenesis on sex ratio is statistically significant, it does not coincide with the theoretical one. Thus, in some cases although the shift of the sex ratio in the experiment in direction of decrease versus the control coincides with the theoretical expectation, it is only with respect to direction. In fact it is, as a rule, insignificant and much weaker than expected on the basis of the size of X chromosome whose contribution to the genome of D. melanogaster makes up about 19%.

The mean sex ratio in culture in experimental samples was 1.085 ± 0.029 (0.985 – 1.614), in control ones it was 1.058 ± 0.013 (1.021 – 1.138), and in all samples 1.071 ± 0.015. Regression analysis of the dependence of the mean sex ratio in cultures on the irradiation dose for males gives a value of regression coefficient . The value for Student test  is equal to , so that the hypothesis that the coefficient of regression is zero is not rejected. The average sex ratio at all the doses remains the same. Since the treatment of males with mutagens does not cause any decrease of sex ratio even at high doses, and yet the influence of mutagens on the sex ratio is statistically significant, we face here a case when there is dependence but no correlation. So what does this dependence consist in?

At first it seemed that mutagenesis increased the variability of sex ratio across cultures of the sample, but this is not the case. Coefficient of correlation between the irradiation dose and characteristics of sex ratio variability in cultures are  for standard deviation , and  for coefficient of variation  at 10 degrees of freedom. The hypothesis of absence of correlation is not rejected. Therefore, the variability of sex ratio does not correlate with the dose, the average value does not correlate, either. Irradiation does not increase the sex ratio variability in the sample, but simply makes the distribution of sex ratio on the whole unstable, influencing irregularly all its characteristics.

We see that the formula of Catcheside and Lea does not describe the dependence under discussion. Our experiments cover a time stretch of about quarter of a century, they were made under various conditions, but, as variance analysis demonstrated, this has not affected the sex ratio. The absence of influence of other conditions than mutagenic treatment of males shows that equal results of the first researchers were not at all caused by similarity of external conditions under which they performed their observations. Similarity of conditions might consist in the fact that at the beginning, when the fly cultivation technique was just starting to be spread, equal procedures, strains, media, temperatures and other factors could be used, which could result in equal effects on the sex ratio. Why did the first researchers observe an equal direction of shift of the sex ratio, remains an enigma. Could it not be a result of prejudice unconsciously widespread in a mysterious way? Is it not surprising that X and Y spermia seem to bring into the zygote an equal number of induced DLM, despite the large difference in their genetic contents, and could one have supposed this a priori? One can hardly doubt, however, as to our experimental data, which seem to meet all the requirements of reliability. Science knows the existence of latent, subconscious and unpremeditated tendentiousness (Taylor, 1987) when a researcher becomes like a seller who has been noticed, when settling accounts, to be mistaken in his own favor. It cannot be ruled out it is just this that has determined the slight shift of sex ratio in our first experiments of 1977, 1979 and 1982 on estimation of the number of DLM (Ivanov, 1998a, b).

In connection with the phenomenon of equal mortality of sexes in mutagenesis, it became necessary to revise the earlier obtained results associated with the estimation of the number of DLM by the sex ratio, and the method (formulae) of their calculation by zygotes’ survival (Ivanov, 1998a, b, c). The error consisted in the fact that, ignoring large errors of the results obtained by the sex ratio, we added and averaged all the data on the number of DLM in order to minimize the total error. It is only thanks to the fact that the averaging was performed with weights inverse to square errors, that the total result did not deviate much from the more correct experimental value. Now that it has become clear that we ought not to pool the results, we have discarded the unreliable data obtained from the sex ratio and used for estimation of the number of DLM by the survival of zygotes the results of an additional experiment discarded earlier because of the considerable chance mortality. Since in the zygote survival method the chance mortality, which is equal in the control and in the experiment, is ruled out, its value does not influence the result. The additional experiment was not analyzed at its time and was ignored for a long time as a failure. The data of this experiment on estimation of the average number of DLM in the genome of D. melanogaster, both spontaneous and induced with the dose of 1500 R, are presented in Table 3. The theory and technique of this experiment are described in our earlier work (Ivanov, 1998c).

Now the calculations have been simplified. In them, only one, average, or intermediate, genome figures, because the necessity of considering two genomes – complete (with X chromosome) and incomplete (with Y chromosome) – has disappeared: both of them bring into the zygote on the average equal numbers of DLM, which follows from all our experiments on the influence of mutagenesis on the sex ratio. The formula for the mean number  of spontaneous DLM in the genome now is as follows

                                    ,                                                                   (5)

where  and  are the mean survival of zygotes in culture in the experiment and in the control, respectively, and  and  are mutability in males’ X chromosome in the experiment and in the control, respectively. The mean number  of induced DLM in the genome is

                                    .                                                                   (6)

The results in Table 3b have been calculated by formulae (5) and (6), however, one can specify them.

            Given the dependence of the average number of mutations induced in males’ X chromosome on the irradiation dose as linear function (2), we shall find the dependence of multiplicity of increase of the number of mutations over the spontaneous level  on the irradiation dose as a linear function

            .                                            (7)

(The estimate of dispersion of multiplicity  at the dose  is .) Then the average number of spontaneous DLM in the genome is

            ,                                                                        (8)

and the mean number of DLM induced in the genome after irradiation of males is .

The errors of calculations by formula (8) are estimated more simply and correctly, so we recalculated by it the average number of spontaneous and induced DLM in the genome in both experiments. At the dose of 1500 R which was used, the multiplicity of increase of the number of mutations is ; the mean number of spontaneous DLM in the genome is  in the experiment with a low chance mortality , and  in the additional experiment with a high chance mortality ; the mean number of DLM in the genome irradiated with 1500 R is  in the former experiment and  in the latter. A weighted averaging of respective data by formula  results in the following estimates, which may be used for practical calculations.

The weighted mean number of spontaneous DLM in the genome is

                        .                                                                         (9)

The weighted mean number of DLM induced in the genome by the dose of 1500 R is

            .                                                              (10)

From the data of (9) and (10), dependence of the mean number of DLM induced in the genome on the dose of irradiation of males is deduced as linear function

            ,            (11)

in which coefficients with errors are  and . Other researchers measured the number of DLM not as their mean number in the genome, but estimated it directly by the death of zygotes (Catcheside, Lea, 1945; Fano, Demerec, 1941). That is why they never observed the simple linear dependence on the dose. From it, formulae for calculation of zygotes’ survival at various doses of irradiation of parent of one sex or of both sexes together are deduced.

Let us assume that irradiation of males and females makes the same DLM contribution to their  progeny. Let us ignore the chance death, i.e. assume it to be zero. If it becomes necessary for correction of the survival value, it will to be easy to introduce it into our formulae as a multiplier . The probability of survival is the probability of formation of a DLM-free zygote. If, as it is assumed,  and  are mean DLM numbers in the genome in spontaneous and induced mutagenesis, respectively, then, due to irradiation of one parent with the dose  the survival of zygotes is , and with irradiation of both parent . Substituting into these expressions the estimate (9) of the number  of spontaneous DLM, and instead of  its expression (11), we shall obtain the dependence of survival of zygotes on the irradiation dose:

 with irradiation of one parent and

 with irradiation of both parents.

So, when males are irradiated with the dose of 15000 R, then , i.e. about  of  zygotes survive (are free from DLM); therefore, in order to obtain in culture the same number of flies as without irradiation, one has to increase the number of parental females by more than 20 times.

The work “Factors of spontaneous mutation, mutability in large chromosomes, and mortality from dominant lethals in D. melanogaster” (Ivanov, 1999) also requires some corrections. The decomposition of the mutation process in the genome of D. melanogaster was practically not changed, but the formulae for calculation of zygotes’ mortality from DLM by mutability in the given chromosome became simplified and partially turned out to be superfluous due to similarity in survival of sexes. Let us deduce them again.

If  is the frequency of occurrence of DLM in the genome, then the mortality of zygotes from DLM, according to the new statement, is equal in both sexes and equal to

                        .                                                         (12)

We shall find the  value by the frequency  of arising of RLM and VM in the -th chromosome and by its proportion  in the whole genome. Let  be the arising frequency of RLM and VM in the whole genome. We have  and, according to the decomposition of the mutation process, . Then , , and the sought mortality of zygotes (12) is

                        ,                                                           (13)

which coincides with the previous formula of mortality for females. The shares of X chromosome and chromosome 2 in the genome are  and , respectively. Substituting these numbers into formula (13), we obtain for each chromosome the expression of the zygotes’ mortality on DLM as a function of mutability in the given chromosome:

                        ;                                                                     (14)

                        .

One can obtain an estimate of the maximal mortality of zygotes from DLM in populations by means of substituting into formulae (14) the highest rates of spontaneous mutability  which are known for these chromosomes:  and . The highest values for mortality from DLM are  and . Hence the spontaneous mutability completely caused by biotic factors (Ivanov, 1998a, 1999) is one of important factors of mortality and of limitation of the numbers of species.

Finally, let us consider the experiments on irradiation of  females (Table 2). Their statistical treatment has led to the following conclusions.

The test for homogeneity of  for the total sex ratio in all the 5 samples, experimental and control ones, shows that the homogeneity hypothesis is not rejected:  at . Experimental samples do not differ from control in the total sex ratio.

Simple one-way variance analysis for checking the equality of average values, and two-way analysis where irradiation and general experimental conditions are the factors demonstrate that irradiation does influence significantly the mean sex ratio in sample cultures at the significant level of , whereas the general conditions do not.

Like in irradiation of males, the influence of irradiation of females on the distribution of sex ratio across  cultures consists in destabilization of the mean sex ratio in absence of its shift in the direction of increase with an increase of the dose, i.e. a shift expected theoretically.

The mean sex ratio in experimental samples was 1.174 ± 0.038 (1.075 – 1.303), in control samples it was 1.090 ± 0.026 (1.063 – 1.138), and over all the samples it was 1.138 ± 0.024. Regression analysis of dependence of the sex ratio on the dose of irradiation of females gives the value for coefficient of regression . The value for Student test  is , i.e. the coefficient of regression is not significantly different from zero, and the mean sex ratio is practically independent of the dose.

The phenomenon of weak dependence of sex ratio on the dose of irradiation of  females with conservation of a value close to unit or to the level without irradiation seem not to have been noticed earlier, otherwise, on the strength of its paradoxical character, it would have raised some problems. The absence of an elevated mortality of males that originated from mutagen-treated ova is extremely puzzling.

First of all, doubts arise as to whether irradiation has taken place. People who worked on the g-irradiator strongly protested against the hypothesis that the IGUR-1 device with caesium-137 that was used worked poorly, since the radiation supervisor regularly controls its power necessary for calculation of irradiation time by the dose, or the dose by the time. At considerable doses, irradiation effect must be well noticeable by the death of flies from DLM. Although we took measures that the number of flies in cultures were considerable and should not be different in the experiment and in the control, i.e. by many times increased the number of parental females in irradiation, yet, as one can judge by the data of the last columns in Tables 1 and 2, the average number of flies in experimental cultures was always smaller than that in the control, so that the effect of irradiation remained noticeable, and there were no reasons to believe that irradiation was absent.

It remains to consider other, non-technical hypothesis. Had not the ova a higher radioresistance than spermia with respect to mutability, or X chromosome of the ova than autosomes? This question can be studied by means of comparing the respective frequencies of arising of mutations.

Are not ova with mutations in X chromosome discarded from the pool of all the ova by means of any special mechanism? Is it not known that the chromosome bridges arising from crossing-over inside a paracentric inversion in females heterozygous for such an inversion go to polocytes in meiosis?

The store of verifiable ideas is rapidly exhausted, one has to have approaches to their study, and one can but leave this matter to other researchers.

Briefly, the results of the present work can be summarized as follows. In D. melanogaster, treatment of parental individuals with mutagens affects the mean sex ratio in their immediate progeny very weakly and irregularly, so that as the dose increases, no directed shift in sex ratio is observed. From the sex ratio it is not possible to get an idea of the dose of mutagen and of the number of DLM; therefore, it is quite impossible to estimate the number of DLM in the genome by the sex ratio. In this connection, some earlier works of the author in which it is necessary to correct the most important formulae and values associated with estimation of the number of DLM in the genome have been revised. The present work will serve to indicate the reader necessary corrections.

The work confirms the well-known gnoseological principle, which is, however, often violated. In cognition, logic alone is quite insufficient. Speculations, even the most obvious ones, require checking with facts, because the reality turns out to be richer than any imagination. Empirical generalizations can destroy most perfect theories.

Acknowledgments: The author is sincerely grateful to Dr. V.G. Kolpakov for translation of the paper into English, and to Drs. D.A. Afonnikov and T.M. Mishchenko for their help in preparation of the manuscript for publication.

References: Catcheside, D.G., and D.E. Lea 1945, Journal of Genetics 47:1-9; Fano, U., and M. Demerec 1941, Genetics 26:151; Hadorn, E., 1961, In: Developmental Genetics and Lethal Factors, London: Methuen & Co, New York: John Wiley & Sons; Ivanov, Yu.N., 1998, Dros. Inf. Serv. 81:a) 180-186, b) 186-193, c) 193-197; Ivanov, Yu.N., 1999, Dros. Inf. Serv. 82:87-90; McClintock, B., 1941, Genetics 26:234-282; Taylor, I.T., 1987, In: In the Minds of Men, Toronto: TFE Publishing.